¶ Seely categories
A Seely category is a model of linear logic.
In more detail, a Seely category consists of
- a symmetric monoidal closed category ...
- ... with finite products, denoted by and
- a comonad on $\mathcal
- natural isomorphisms (so-called Seely isomorphisms)
such that the diagram
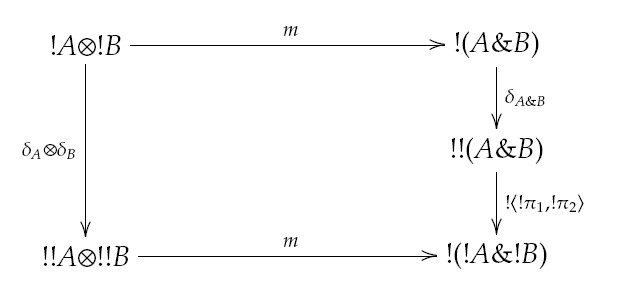
commutes.
¶ As models of Classical Linear Logic
As it stands, a Seely category is a model of intuitionistic Linear Logic. However, the definition can easily be extended to classical linear logic. The key is to ask that the symmetric monoidal closed category is *-autonomous, i.e. that there is an object (the dualizing object) such that the canonical map
given by currying the evaluation map is an isomorphism for every object .
¶ References
- An exposition of Seely categories is given in §7.3 of
Melliès, Paul-André. 2009. ‘Categorical Semantics of Linear Logic’. In Panoramas et Synthèses 27: Interactive Models of Computation and Program Behaviour, edited by Pierre-Louis Curien, Hugo Herbelin, Jean-Louis Krivine, and Paul-André Melliès. Société Mathématique de France. [pdf]
@incollection{mellies_categorical_2009,
title = {Categorical {Semantics} of {Linear} {Logic}},
isbn = {978-2-85629-273-0},
url = {http://www.pps.univ-paris-diderot.fr/~mellies/papers/panorama.pdf},
booktitle = {Panoramas et synthèses 27: {Interactive} models of computation and program behaviour},
publisher = {Soci\'{e}t\'{e} Mathématique de France},
author = {Melliès, Paul-André},
editor = {Curien, Pierre-Louis and Herbelin, Hugo and Krivine, Jean-Louis and Melli\`{e}s, Paul-Andr\'{e}},
year = {2009}
}
¶
- As evident in the name, the original (slightly faulty) definition of Seely categories is due to Robert Seely.
Seely, R. A. G. 1989. ‘Linear Logic, *-Autonomous Categories and Cofree Coalgebras’. In Categories in Computer Science and Logic, 92:371–82. Contemporary Mathematics. Boulder, Colorado: American Mathematical Society.
@inproceedings{seely_linear_1989,
address = {Boulder, Colorado},
series = {Contemporary {Mathematics}},
title = {Linear {Logic}, $*$-{Autonomous} {Categories} and {Cofree} {Coalgebras}},
volume = {92},
booktitle = {Categories in {Computer} {Science} and {Logic}},
publisher = {American Mathematical Society},
author = {Seely, R. A. G.},
year = {1989},
pages = {371--382}
}
¶
- The definition given here is sometimes referred to as a "new Seely category, and is a technical improvement upon Seely's original definition. It is due to Gavin Bierman: it appeared in his 1993 PhD thesis, and then was published in
Bierman, G. M. 1995. ‘What Is a Categorical Model of Intuitionistic Linear Logic?’ In Typed Lambda Calculi and Applications, edited by Mariangiola Dezani-Ciancaglini and Gordon Plotkin, 902:78–93. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer Berlin Heidelberg. https://doi.org/10.1007/BFb0014046.
@inproceedings{bierman_1995,
address = {Berlin, Heidelberg},
series = {Lecture {Notes} in {Computer} {Science}},
title = {What is a categorical model of {Intuitionistic} {Linear} {Logic}?},
volume = {902},
isbn = {978-3-540-59048-4 978-3-540-49178-1},
doi = {10.1007/BFb0014046},
booktitle = {Typed {Lambda} {Calculi} and {Applications}},
publisher = {Springer Berlin Heidelberg},
author = {Bierman, G. M.},
editor = {Dezani-Ciancaglini, Mariangiola and Plotkin, Gordon},
year = {1995},
pages = {78--93}
}
¶
See more discussion in §7.7 of [Mellies 2009].